Selection Sort
Selection sort is one of the O(n2) sorting algorithms where the minimal value is put in the start of the array. This sorting algorithm is inefficient on large lists, and generally performs worse than the similar insertion sort due to its computational complexity.
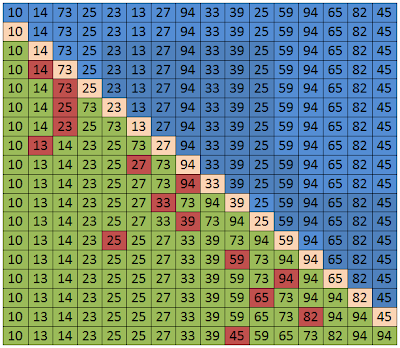
In selection sort, the array of inputs is imaginatively divided into two parts, the sorted and unsorted part. At the beginning, the sorted part is empty and the unsorted part is the whole array. In every loop, the algorithm looks for the smallest number from the unsorted array and then would swap it to the first element of the unsorted part. The loop stops until the unsorted part is empty.
Example. {10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45}
The C++ codes for the selection sort are the following:
int i, j, minIndex, tmp;
for (i = 0; i < n - 1; i++) {
minIndex = i;
for (j = i + 1; j < n; j++)
if (arr[j] < arr[minIndex])
minIndex = j;
if (minIndex != i) {
tmp = arr[i];
arr[i] = arr[minIndex];
arr[minIndex] = tmp;
}
}
}
###########
Insertion Sort
Insertion sort is a simple sorting algorithm in which, just like the selection sort, belongs to the O(n2) sorting algorithms. It is a comparison sort in which the sorted array is built one entry at a time.It is much less efficient on large lists than more advanced algorithms such as quicksort, heapsort, or merge sort. However, it has a simple implementation and is efficient for small data sets.
Insertion sort works like selection sort. The array is also divided imaginatively into two parts. The sorted part is the array containing the first element and the unsorted part contains the rest of the inputs. In every loop, the algorithm inserts the first element from the unsorted part to its right position in the sorted part. And the loop ends when the unsorted part is empty.
Example. {10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45}
The C++ codes for the insertion sort are the following:
void insertionSort(int arr[], int length) {
int i, j, tmp;
for (i = 1; i < length; i++) {
j = i;
while (j > 0 && arr[j - 1] > arr[j]) {
tmp = arr[j];
arr[j] = arr[j - 1];
arr[j - 1] = tmp;
j--;
}
}
}
int i, j, tmp;
for (i = 1; i < length; i++) {
j = i;
while (j > 0 && arr[j - 1] > arr[j]) {
tmp = arr[j];
arr[j] = arr[j - 1];
arr[j - 1] = tmp;
j--;
}
}
}
###########
Bubble Sort
Bubble sort is a simple and well-known sorting algorithm. Bubble sort belongs to O(n2) sorting algorithms, which makes it quite inefficient for sorting large data volumes. Bubble sort is stable and adaptive.
Bubble sort works by comparing pair of adjacent elements from the beginning of an array and tests them if they are in reversed order. If the current element is greater than the next element, then the algorithm swaps them. The algorithm stops when there are no more elements to be swapped.
Example. {2 3 4 5 1}
The C++ codes for the insertion sort are the following:
void bubbleSort(int arr[], int n) {
bool swapped = true;
int j = 0;
int tmp;
while (swapped) {
swapped = false;
j++;
for (int i = 0; i < n - j; i++) {
if (arr[i] > arr[i + 1]) {
tmp = arr[i];
arr[i] = arr[i + 1];
arr[i + 1] = tmp;
swapped = true;
}
}
}
}
bool swapped = true;
int j = 0;
int tmp;
while (swapped) {
swapped = false;
j++;
for (int i = 0; i < n - j; i++) {
if (arr[i] > arr[i + 1]) {
tmp = arr[i];
arr[i] = arr[i + 1];
arr[i + 1] = tmp;
swapped = true;
}
}
}
}
###########
Shell Sort
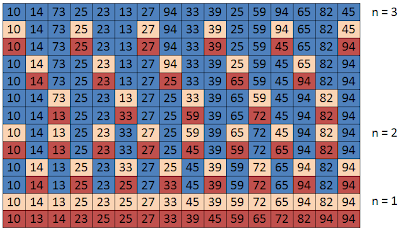
Shell Sort is one of the oldest sorting algorithms which is named from Donald Shell in 1959. It is fast, easy to understand and easy to implement. However, its complexity analysis is a little more sophisticated. Shell sort is the generalization of the insertion sort which exploits the fact that insertion sort works efficiently on input that is already almost sorted.
Shell sort algorithm does not actually sort the data itself but it increases the efficiency of other sorting algorithms, normally is the insertion sort. It works by quickly arranging data by sorting every nth element, where n can be any number less than half the number of data. Once the initial sort is performed, n is reduced, and the data is sorted again until n equals 1.
Choosing n is not as difficult as it might seem. The only sequence you have to avoid is one constructed with the powers of 2. Do not choose (for example) 16 as your first n, and then keep dividing by 2 until you reach 1. It has been mathematically proven that using only numbers from the power series {1, 2, 4, 8, 16, 32, ...} produces the worst sorting times. The fastest times are (on average) obtained by choosing an initial n somewhere close to the maximum allowed and continually dividing by 2.2 until you reach 1 or less. Remember to always sort the data with n = 1 as the last step.
Example. {10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45}
The C++ codes for the insertion sort are the following:
void shellsort (int[] arr, int length, int n) {
int i, j, k, h, v;
for (k=0; k < length; k++) {
h=arr[k];
for (i=h; i<n; i++) {
v=arr[i];
j=i;
while (j>=h && arr[j-h]>v) {
arr[j]=arr[j-h];
j=j-h;
}
arr[j]=v;
}
}
}
int i, j, k, h, v;
for (k=0; k < length; k++) {
h=arr[k];
for (i=h; i<n; i++) {
v=arr[i];
j=i;
while (j>=h && arr[j-h]>v) {
arr[j]=arr[j-h];
j=j-h;
}
arr[j]=v;
}
}
}
Source:



No comments:
Post a Comment